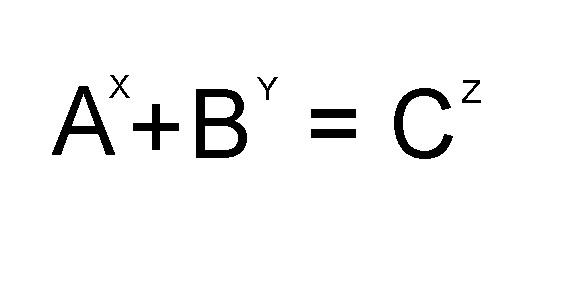01 Numeros y Simbolos en Matematicas: 
01 ¿Que Tipos de Numeros y Simbolos Existen?
01 Definicion de Numero y Tipos de Numeros Que Existen
Cuando nos referimos a un número, esté número, suele ser un número natural de base 10 que es en la que contamos, y esté número, esta construido de manera lógica con dígitos numéricos repetidos o no, que van de derecha a izquierda, y que expresados de manera coherente, expresan un valor de unidades únicas ( de 1 ), repetidas o no, y además, ese valor puede valer nada, o, valer de una a varias unidades básicas expresadas con esos dígitos que a partir de 2 son grupos de unidades repetidas.
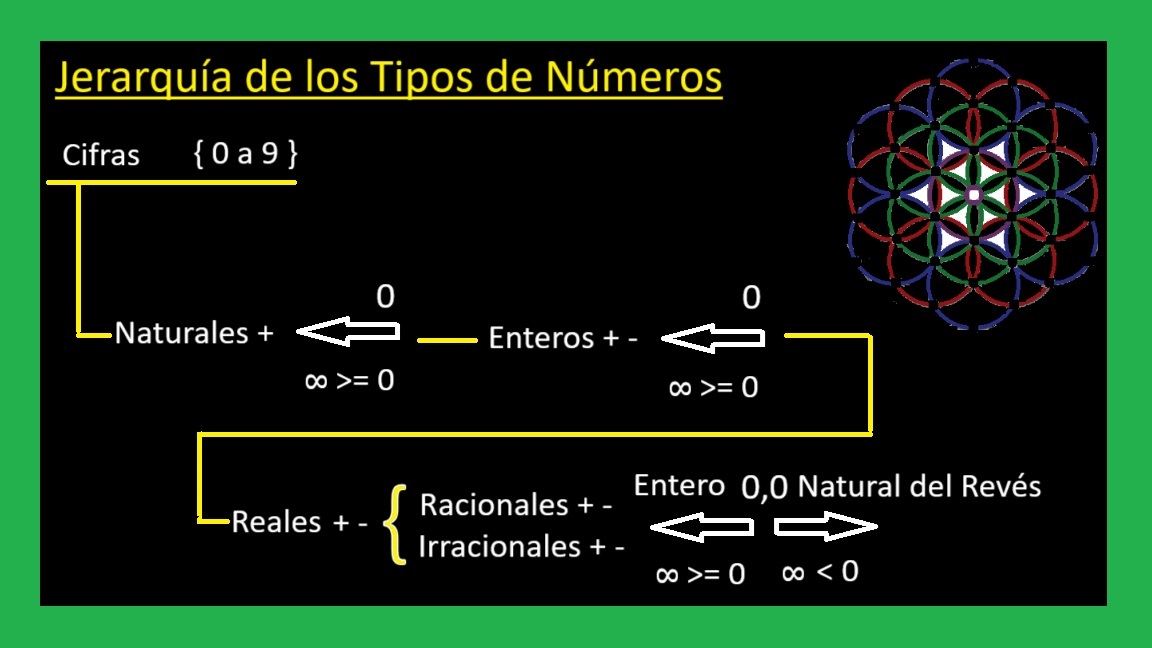
- Los naturales de un número sin signo.
- Los enteros de un número con y sin signo.
- Son únicos y unidireccionales ( van de derecha a izquierda y no contienen parte fraccionaria ).
- Los racionales e irracionales de dos números el primero entero con y sin signo y el segundo natural al revés.
- Son duales y bidireccionales ( el 1º es un entero de derecha a izquierda, y, el 2º , que es un natural al revés, va de izquierda a derecha ).
Existen muchos tipos de número que utilizan en su definición estas 2 clases de 4 tipos de números principalmente, y aquí, te muestro algunos ejemplos de todos ellos:
- Que es un número y tipos de números que existen.
- Tipo 1 Todas las Bases: Los números naturales y los números enteros.
- Tipo 2 Base 10: Los números fraccionarios.
- Tipo 2 Base 10: Los números racionales.
- Tipo 2 Base 10: Los números irracionales.
- Tipo 2 Base 10: Los números reales.
- Enteros y Reales Base 10: Los números imaginarios o números complejos.
- Enteros y Reales Base 10: Los números simétricos.
- Enteros y Reales Base 10: Los números asimétricos.
- Naturales Base 10: Los números pares e impares.
- Naturales Base 10: Los números primos.
- Naturales Base 2: Los números binarios.
- Naturales Base 8: Los números octales.
- Naturales Base 16: Los números hexadecimales.
- Naturales Base 10: Los números amigos.
- Naturales Base 10: Los números perfectos.
- Irracionales Base 10: Los números trascendentes.
- Naturales Base 10:Los números taxicab.
- Irracionales Base 10: Los números periódicos.
- Enteros y Reales Base 10: Los números inversos.
- Enteros y Reales Base 10: Los números reversos.
- Enteros y Reales Base 10: La Fractalidad de los Operadores en Pol Power Calculator.
- Constante Irracional Base 10: El número PI.
- Constante Irracional Base 10: El número E de Euler.
- Constante Irracional Base 10: El número Aureo.
Cada uno de todos ellos se explican a continuación:
02 Definicion de Numeros Naturales y Numeros Enteros
Todos los números con los que contamos cosas habitualmente, los situaríamos en la base 10 , y, cómo números naturales, ya que es con estos, con los que contamos algo físico o no, que es de alguna forma una repetición de esas unidades básicas, que representan un número de veces el objeto físico o no, igual a los otros o no, y que con un máximo de 10 dígitos simbólicos ( por la base 10 ) los repetimos , y que, con estos, se expresa un valor de grupo de unidades repetidas con las que expresamos valores de grupo.
Así, todos los números naturales de cualquier base son: el objeto inicial de 0 y 1 , que más sus dígitos simbólicos, si es que los tiene, expresan repeticiones en esa base, con lo que se puede expresar algo con algún valor grupal en especial, que expresa un valor de grupo de unidades de 1 repetidas en una cierta base de dígitos simbólicos, y que al repetir-los, genera números en esa base.
Los números enteros, son todos aquellos números, que además de poder ser números naturales ( cero uno o valor grupal ), pueden ser su mismo valor en negativo ( Lo mismo pero en negativo ).
- { 0 = Ausencia de Unidad Básica } = Cruce adimensional que señala posición pero sin contenido dimensional.
- { 1 = Existencia de Unidad Básica } = Entidad Punto que señala posición y contenido dimensional.
- { 0 1 2 3 4 5 6 7 8 9 } Estos son los 10 dígitos simbólicos usables y que se repiten por grados a la derecha en la base 10.
- { 1 2 3 4 5 6 7 8 9 } 1er Grado de la Izquierda.
El 10 encaja con su propio valor siguiendo la cadena de números en la base 10 de números contables.
- { 2 3 4 5 6 7 8 9 } Números de posibles bases numéricas por poner un ejemplo.
Aquí son un total de 8 valores de grupo por esto es octal en su primer grado, y decimal en los siguientes grados que repetimos.
- Segundo Grado u Orden { X0 X1 X2 X3 X4 X5 X6 X7 X8 X9 } donde X es grado a la izquierda de natural contable de primer grado u orden, siendo el conjunto un número de 2 grados.
- Tercer Grado u Orden { XY0 XY1 XY2 XY3 XY4 XY5 XY6 XY7 XY8 XY9 } donde X es grado a la izquierda natural contable de primer grado u orden, e Y es grado a la derecha, y es un número con alguno de los 10 dígitos simbólicos de base 10 donde el conjunto de ellos hace un número de 3 grados.
- Los siguientes grados son más de lo mismo del tercero extendido al número de grados que puedas manejar ya que estos así es un largo etc...
- Naturales y Enteros Positivos { 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +11 +12 ... +Infinito }
- Solo Enteros Negativos { 0 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 ... -Infinito }
- Naturales y Enteros Positivos { +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +11 +12 ... +Infinito }
- Solo Enteros Negativos { -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 ... -Infinito }
- Naturales y Enteros Positivos de Valor de Grupo { +2 +3 +4 +5 +6 +7 +8 +9 +10 +11 +12 ... +Infinito }
- Solo Enteros Negativos de Valor de Grupo { -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 ... -Infinito }
03 Definicion de Numeros Fraccionarios
Los números fraccionarios, los solemos expresar en base 10 , cómo una operación de división, que expresamos con un par de números naturales de base 10 divididos entre si.
El primer número es el numerador y el número que la divide le llamamos denominador.
La fracción puede dar cómo resultado un número entero o racional, cuando son simetricamente exactas, e irracional, cuando son asimétricas e infinitas.
Ejemplos de fracciones exactas con resultados de números naturales y racionales positivos:
Números de Fracción = Resultado
Numerador / Denominador = Resultado.
9/3 = 3
4/2 = 2
1/1 = 1
1/2 = 0,5
3/4 = 0,75
1/5 = 0,2
1/8 = 0,125
1/10 = 0,1
etc...
Ejemplos de fracciones infinitas con error por defecto ( de números asimétricos ) con resultados de números irracionales:
Numerador / Denominador = Resultado.
10/3 = 3,33333333... con 3 periódico.
1/3 = 0,33333333... con 3 periódico.
1/6 = 0,16666666... con 6 periódico.
1/9 = 0,11111111... con 1 periódico.
etc...
04 Definicion de Numeros Racionales
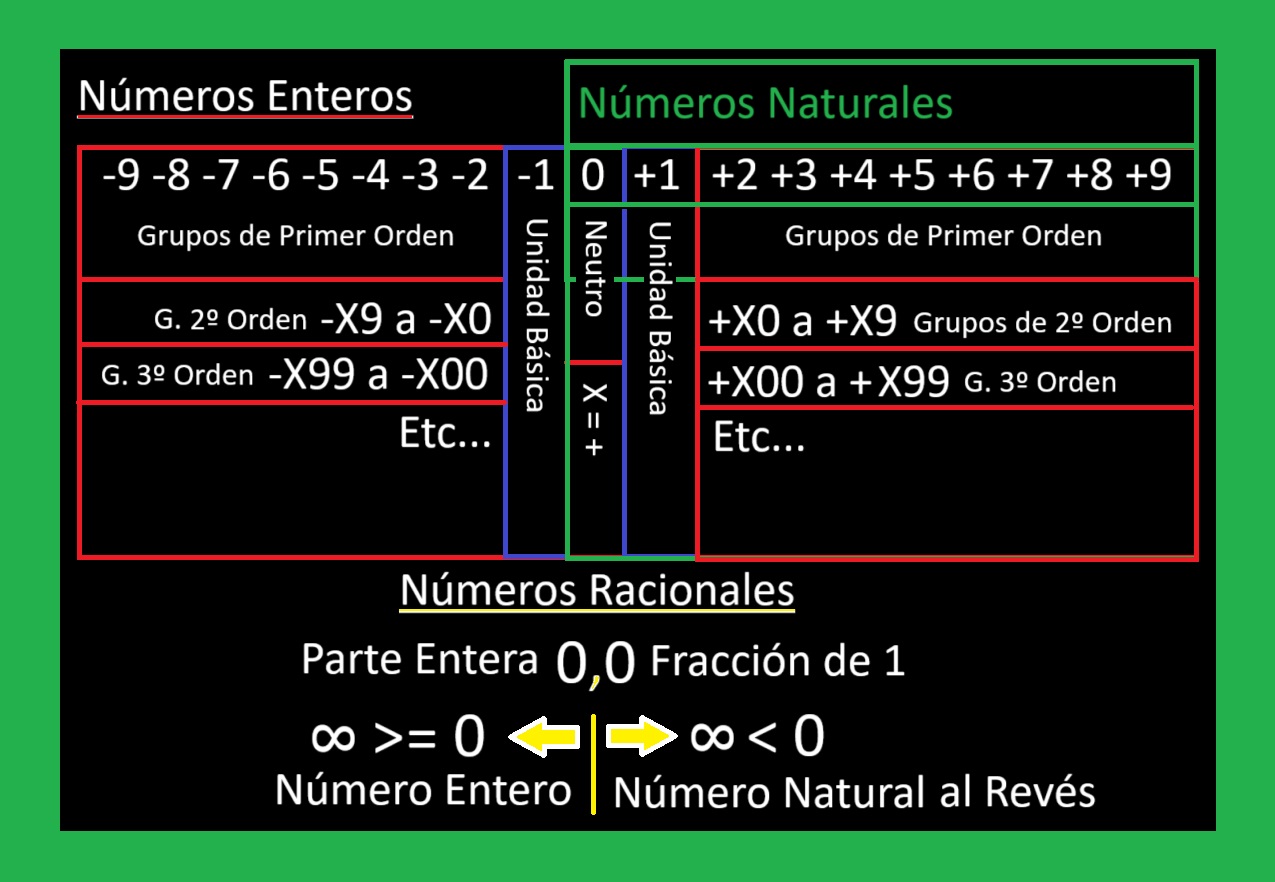
Los números racionales, son todos aquellos números en base 10 , compuestos de un par de números, uno entero y otro natural, que seguidos pero separados por una coma, indican en la parte izquierda, una parte entera, que es mayor o igual a 0 , y que además, tiene un segundo número natural puesto del revés y en la parte derecha de la coma que indica una fracción de 1 en formato de número inverso.
Así esto queda de la siguiente forma:
X |,| Y = X,Y
X = Derecha a Izquierda de Menor a Mayor | Y = Izquierda a Derecha de Mayor a Menor
X = Infinito >= 0 | Y = Infinito < 0
X = Parte Entera | Y = Fracción de 1/Y
Estos son todos los ejemplos de números entre 0 y 1 , que son racionales, salidos de fracciones y que indican partes exactas:
Numerador / Denominador = Resultado Racional
1/8 = 0,125
1/5 = 0,2
1/4 = 0,25
3/8 = 0,375
2/5 = 0,4
1/2 = 0,5
3/5 = 0,6
5/8 = 0,625
3/4 = 0,75
4/5 = 0,8
7/8 = 0,875
Estos son los ejemplos de números fraccionarios, que su solución son estos números racionales y reales de fracción similar con mismo resultado:
{ 1/2 = 0,5 } = { 2/4 = 0,5 } = { 4/8 = 0,5 }
{ 3/4 = 0,75 } = { 6/8 = 0,75 }
Etc...
05 Definicion de Numeros Irracionales
Los números irracionales, son números racionales, que con algún operador de función, crea números infinitos, siendo la parte derecha del número racional una parte infinita en su resultado.
Estos son algunos ejemplos de ecuaciones irracionales con ejemplos de entre 0 y 1:
Numerador | Denominador = Resultado Irracional
1|9 = 0,111111111111... con 1 periódico
1|7 = 0,142857142857... con 142857 periódico
1|6 = 0,166666666666... con 6 periódico
2|7 = 0,285714285714... con 285714 periódico
1|3 = 0,333333333333... con 3 periódico
3|7 = 0,428571428571... con 428571 periódico
4|9 = 0,444444444444... con 4 periódico
2|3 = 0,666666666666... con 6 periódico
Estos son ejemplos de números irracionales de la función de raíz:
Radicando yRoot Base = Resultado Irracional
2 yRoot 2 = 1,414213562373...
8 yRoot 2 = 2,828427124746...
06 Definicion de Numeros Reales
Los números reales son el conjunto de números racionales, y, de números irracionales, agrupados ambos bajo el mismo nombre o definición cómo "números reales".
Ejemplos de Números Reales:
2,525 donde 2 es su parte entera y de 525 de parte decimal
10,3875 donde 10 es su parte entera y 3875 de parte decimal
1,1666... con 6 Periódico donde 1 es su parte entera, con 6 de parte decimal periódica
07 Definicion de Numeros Imaginarios o Numeros Complejos
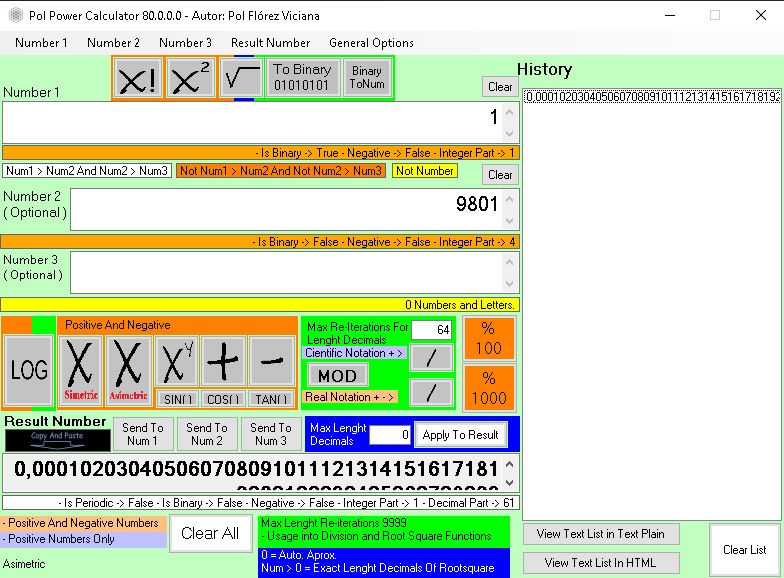
El número imaginario es la unidad básica en si ( el 1 ), pero, en negativo, y está se creó de no existir números negativos en las potenciaciones de exponente par y raíces de base par de otras calculadoras, donde las calculadoras Pol Power Calculator esto no pasa así.
En las calculadoras Pol Power Calculator este comportamiento está correjido, ya que el signo depende de las entradas de base y exponente en potencia o base y radicando en la raíz, tratando-las cómo pasa en una multiplicación, con ley de signos.
De todas formas sigue habiendo el problema de multiplicar seguidos un número de parámetros pares en negativo, que nunca provoca negativos cuando todos los parámetros son negativos, donde esto con parámetros impares no hay problema de signo.
Así el número imaginario corrije este comportamiento haciendo de parámetro impar en una serie de multiplicaciones seguidas de parámetros par.
Elevar algo positivo o negativo por el número imaginario de exponente, invierte el signo de base para su signo inverso de resultado, ya que poner 1 en positivo en el exponente respetaria el signo de base, pero esto, sólo pasa en las calculadoras Pol Power Calculator.
08 Definicion de Numeros Simetricos
Cuando hablo de simetría, es algo que después de un proceso tiene igualdad en el regreso al origen con su inversa.
La simetría de los números simétricos, está en todos los números enteros o racionales, que después de operar con un operador definido cómo multiplicación con división y potencias con raíces o logaritmos u otros ejemplos podemos dar regresión y volver a dar su simetría natural de origen con total exactitud.
Si no hay exactitud es que es asimétríco.
Por ejemplo: Con el 2·3=6 así 6/3=2 y 6/2=3 donde estas ecuaciones son de números simétricos en todos los casos.
Otro ejemplo: Con potencias 2^3=8 y su raíz 2=(8)yRoot(3) y este caso es simetríco.
09 Definicion de Numeros Asimetricos
Los números asimétricos son todos aquellos números que no presentan simetría en sus inversas.
Por ejemplo: El 3,333...=10/3 y entonces 9,999...=3·3,333... así está presenta asimetría.
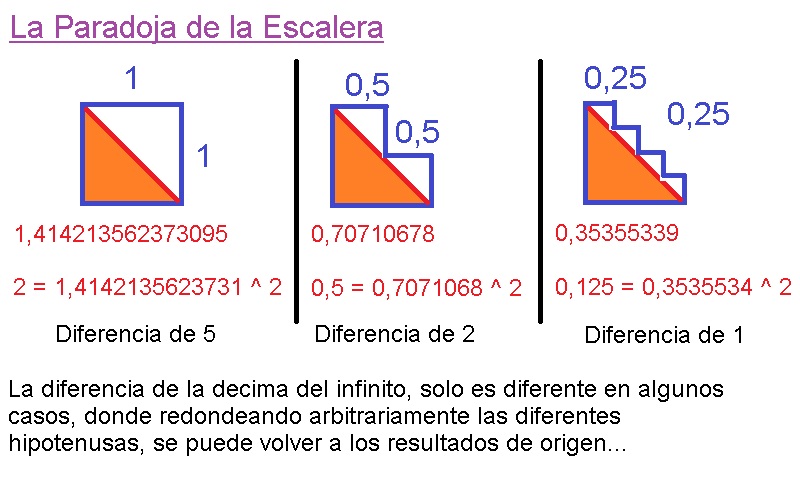
Otro ejemplo: El 1,4142...=(2)yRoot(2) es diferente a 1,4142...^2=1,9999... y no 2 que por tanto la raíz cuadrada de 2 es asimétrica...
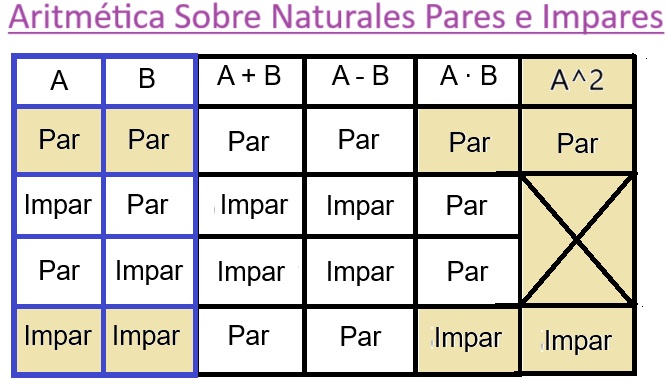
10 Definicion de Numeros Pares e Impares
Los números pares: son todos aquellos números enteros, que en su primer simbolo de su primer dígito de la derecha, contiene uno de estos simbolos { 2 4 6 8 } o el { 0 } , con la excepción de que el { 0 } con más números de primer grado a la izquierda, entonces es par.
Los números impares: son los que en la posición de la derecha del número, sean la resta de simbolos de base 10 del 1 al 9 que no son pares, cómo son el { 1 3 5 7 9 }.
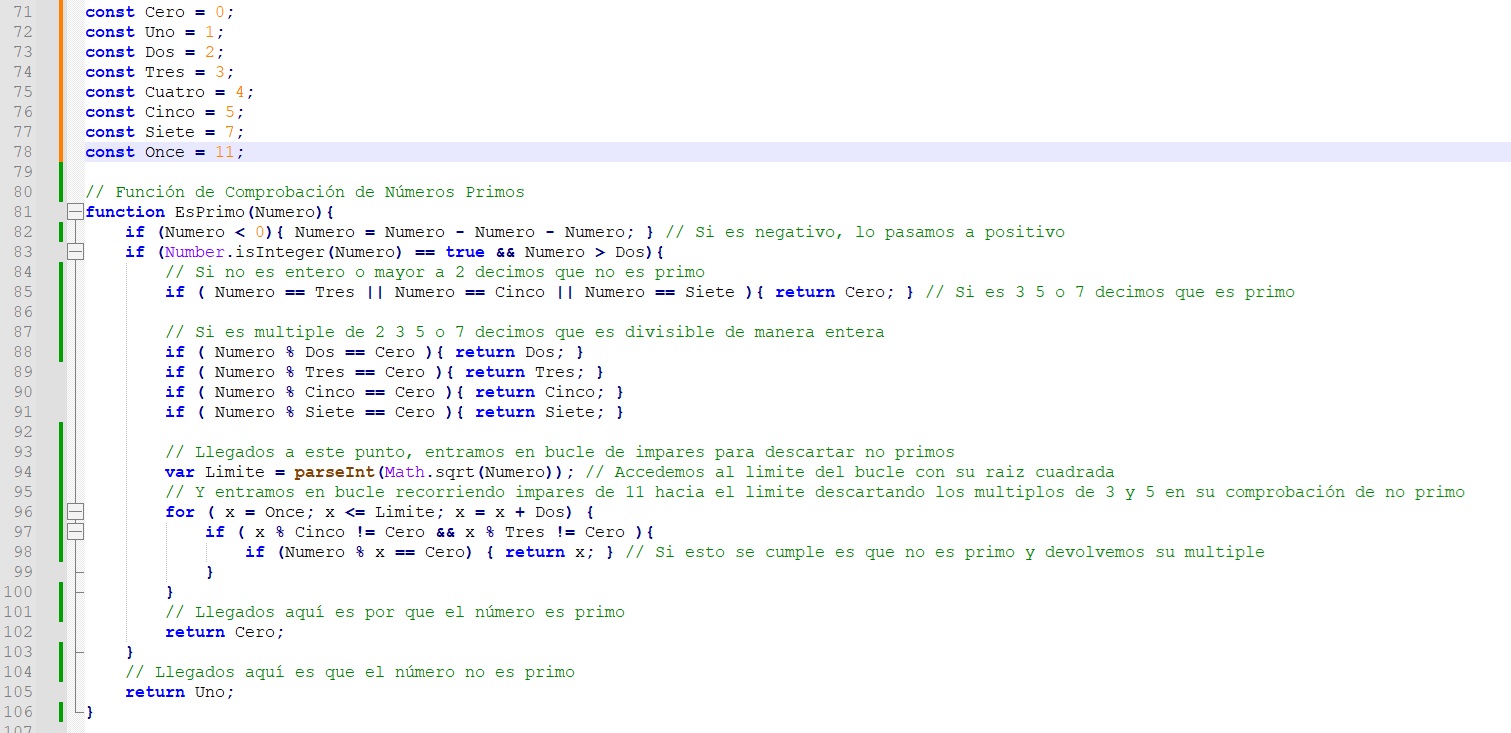
11 Definicion de Numero Primo
Cualquier número entero de valor grupal mayor a 2 e impar, que solo puede ser dividido con resultado entero, entre el número a si mismo, o a 1, se dice que es un número primo.
Números Primos Impares 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , etc...
12 Definicion de Numero Binario
Los números binarios son números en base 2 y eso quiere decir que se componen de 2 dígitos o simbolos ( el 0 y el 1 ).
Estos se pueden combinar en mas de uno de esos simbolos o dígitos, para representar informaciones más complejas cómo ahora números decimales, letras, caracteres o simbolos especiales.
Todos los números enteros pueden representarse de manera binaria y a la inversa.
Ejemplos de números binarios:
Binario = Decimal
0 = 0
1 = 1
10 = 2
11 = 3
100 = 4
1010 = 10
13 Definicion de Numero Octal
Los números octales naturales pertenecen a otra de las base natural muy usadas, la base 8 , que se representa con 8 dígitos simbólicos ( números del 0 al 7 ).
Ejemplos de números octales:
Octal = Decimal
0 = 0
7 = 7
10 = 8
11 = 9
14 Definicion de Numero Hexadecimal
Los números hexadecimales, son números naturales de base 16 definida con números y letras ( dígitos simbólicos ) que siguen la cadena alfabética.
Cada uno de estos dígitos simbólicos está representado con 1 dígito alfanumérico del 0 al 9 y luego se sigue con la letra alfabética de la A a la F del abecedario.
- { 0 1 2 3 4 5 6 7 8 9 A B C D E F } De 0 a 15 consecutivamente
Ejemplos de números hexadecimales:
Hexadecimal = Decimal
0 = 0
1 = 1
2 = 2
...
9 = 9
A = 10
B = 11
...
F = 15
10 = 16
...
FF = 255
...
Etc...
15 Definicion de Numero Amigo
Los números amigos, son una pareja de números enteros, cuyos divisores enteros positivos sumados, den el número del amigo.
Por ejemplo: 220 y 284 son números amigos por lo siguiente:
Para el amigo 220 tenemos que los divisores de 220 son 284 = 1+2+3+4+5+10+11+20+22+44+55+110
Para el amigo 284 tenemos que los divisores de 284 son 220 = 1+2+4+71+142
Los números perfectos, son amigos a si mismos.
16 Definicion de Numero Perfecto
Los números perfectos, son todos aquellos números enteros pares, que son la suma de todos sus divisores con resultado entero, sin incluir-se a si mismo.
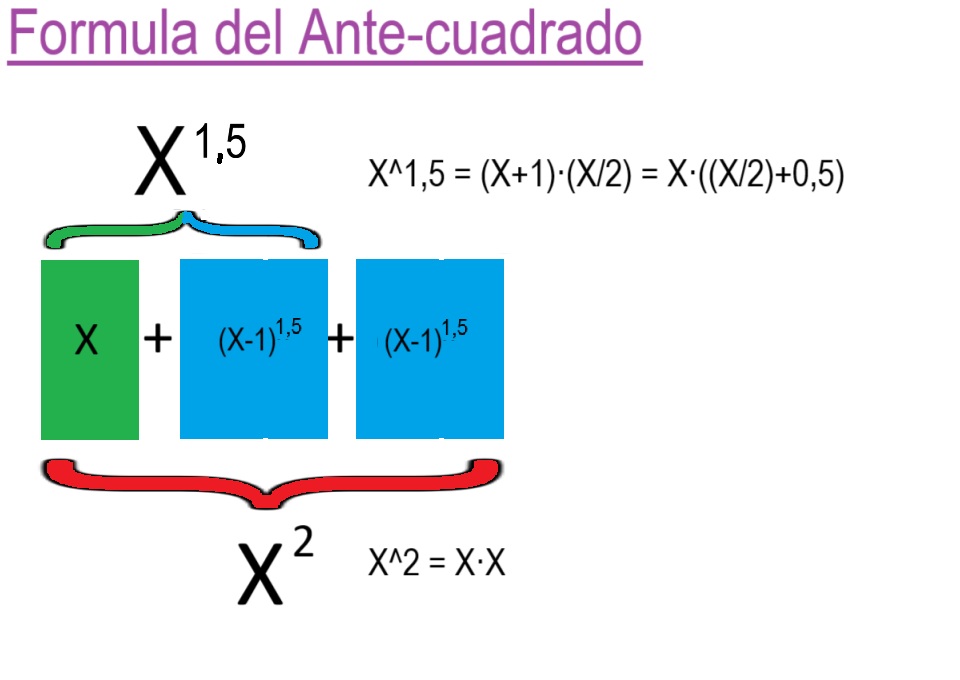
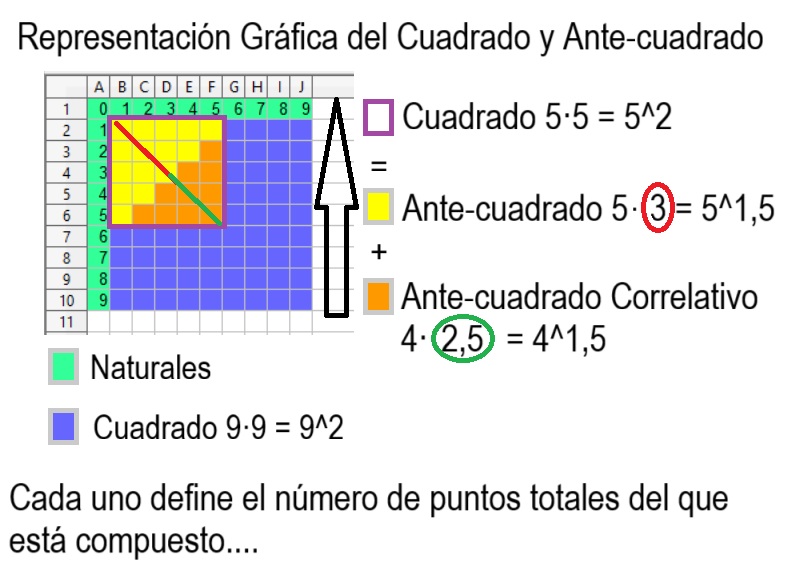
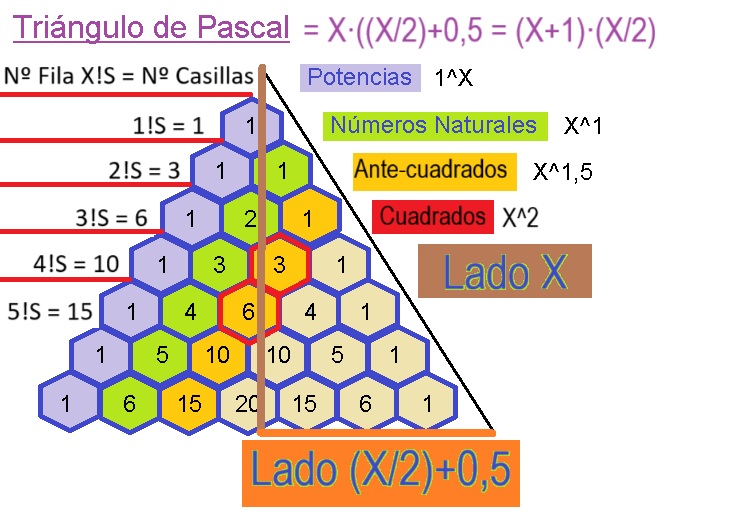
Del mismo modo, el número perfecto, es todo aquel número entero par, que es el resultado de un ante-cuadrado de un número X , donde X es el primero y único de los divisores naturales impares que hay entre los divisores enteros desde la mitad del número perfecto hasta el 1
El número perfecto, es aquel, que es amigo a si mismo.
Así, un número perfecto, cumple lo siguiente, cuando X es un número natural grupal e impar:
Número Perfecto = ((2^X)-1)!S = ((2^X)-1)^1,5 donde X es natural grupal e impar, incluyendo al 2 también, cómo excepción par.
17 Que Son Los Numeros Trascendentes
Los números trascendentes son conocidos cómo números no algebraicos.
Los números trascendentes son números que no pueden escribir-se como una operación algebraica estándar.
Por ejemplo:
La raíz cuadrada de 2 , da un número irracional por tener un número de resultado con 1 número infinito de dígitos, en cambio un número trascendente no puede escribir-se de esta manera, siendo ejemplos de números trascendentes, los números PI o número e de Euler entre otros.
18 Que Son Los Numeros Taxicab
Los números taxicab son los números más pequeños, de la suma de 2 números enteros que elevados al cubo, tienen de 1 a más equivalencias según el orden, con los mismos resultados de otras potencias al cubo.
Por ejemplo, los primeros números taxicab son:
1.- 2 = (1^3)+(1^3)
2.- 1729 = (1^3)+(12^3)
2.- 1729 = (9^3)+(10^3)
3.- 87539319 = (167^3)+(436^3)
3.- 87539319 = (228^3)+(423^3)
3.- 87539319 = (255^3)+(414^3)
4.- 6963472300248 = (2421^3)+(19083^3)
4.- 6963472300248 = (5436^3)+(18948^3)
4.- 6963472300248 = (10200^3)+(18072^3)
4.- 6963472300248 = (13322^3)+(16630^3)
5.- Etc...
19 Que Son Los Numeros Periodicos
Los números periódicos son aquellos números irracionales que salen de una división donde en su fracción de 1 presenta repetición de 1 o varios dígitos en bucle.
Por tanto, un número periódico es un número irracional que en su fracción de 1 devuelve una proporción indeterminada por residuo mayor a 0, y que por esto, se repite en el bucle de una división.
Ejemplos de Números Periódicos:
3,333... con 3 Periódico
6,666... con 6 Periódico
9,999... con 9 Periódico
1,4285714... con 428571 Periódico
20 Definicion de Numero Inverso
Un número inverso, es por definición, que multiplicado por , arroja como resultado la .
En potencias, el inverso de una base suele ser la unidad de 1 , pero, en el inverso del ante-cuadrado la unidad es el valor de base en si misma.
Por ejemplo, el inverso en potencias de base 2 es (1/2)^1 y es esto:
El inverso de 2 es 1/2 = 0,5 Esto es: / =
El inverso de 0,5 es 1/0,5 = 2 Esto es: = ·
Mientras el inverso del ante-cuadrado es:
El inverso del ante-cuadrado de 2 es lo siguiente: = / = 2/1,5
y como la unidad es de 2 pasa que: = ·
21 Definicion de Numero Reverso
El número reverso, es el resultado de que sumado con , resulta en la
Por ejemplo:
- =
= +
22 La Fractalidad de los Operadores en Pol Power Calculator
Algunos operadores son cómo los fractales, tienen la propiedad de autosimilitud.
La propiedad de autosimilitud esta en los resultados de X e Y que son iguales a Z y por lo único que se diferencian es por el signo resultante.
X·Y=Z , -X·-Y=Z , -X·Y=-Z , X·-Y=-Z
X/Y=Z , -X/-Y=Z , -X/Y=-Z , X/-Y=-Z
Esta propiedad de autosimilitud la tiene indiscutiblemente la multiplicación y la división.
Las potencias, raíces y logaritmos en Pol Power Calculator heredan de la multiplicación y la división esta propiedad en la que una operación de 2 números de entrada junto a sus signos es igual que en multiplicaciones y divisiones.
Así los números de estas ecuaciones para estos operadores son cómo los fractales de la naturaleza, en el que cada par de números de entrada reflejan 4 posibles respuestas o soluciones en las salidas, donde entre ellas hay dualidad fractal en cada par ( una es la inversa de la otra en números con signo ).
23 Definicion del Numero PI
La constante PI es un número muy utilizado en operaciones de base 10 en matemáticas, principalmente en geometría y trigonometría.
El número PI define el perímetro de un circulo, y mide la constante de veces el radio del circulo.
El número PI también puede ser interpretado cómo la ecuación de un par de sumatorias, siendo una de un caso mas en veces que la otra, de 2 series de A , donde A es un algoritmo o ecuación diferente según la constante requerida.
El número PI es una constante de número irracional y trascendente, ya que tiene infinidad de dígitos decimales.
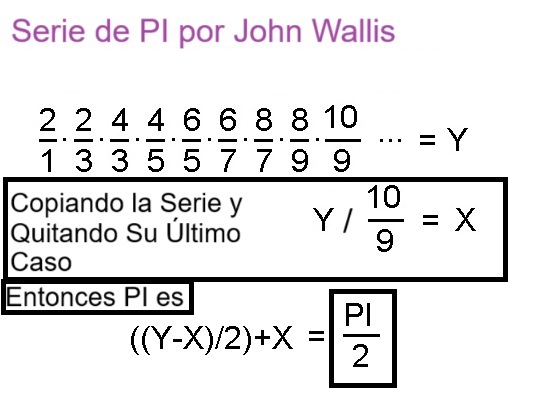
El número PI se puede calcular con el método de John Wallis mediante una serie que a cuantas más iteraciones, más decimales de PI obtendremos:
X = (2/1)·(2/3)·(4/3)·(4/5)·(6/5)·(6/7)·(8/7)·(8/9)...
Y = (2/1)·(2/3)·(4/3)·(4/5)·(6/5)·(6/7)·(8/7)·(8/9)·(10/9)...
PI/2 = ((Y-X)/2)+X
Una buena aproximación del número PI esta en la división de 355/113 con 6 decimales de exactitud.
La constante PI con 49 decimales es la siguiente:
3,1415926535897932384626433832795028841971693993751
24 Definicion del Numero E de Euler
El número E también conocido como número de Euler, fue introducido en 1.731 por el matemático Leonhard Euler, y es una constante de base 10 muy utilizada en matemáticas.
El número E es el resultado de la serie secuencia o sucesión sumatoria de uno dividido por factoriales incrementalmente de unidad en unidad de la forma siguiente:
E = 1+(1/1!)+(1/2!)+(1/3!)+(1/4!)...
Así, el número de Euler, es también una serie secuencia o sucesión de sumatoria un poco especial cómo otras constantes de sumatorias ( la constante PI por ejemplo ).
Esta constante E con 49 decimales es la siguiente:
2,7182818284590452353602874713526624977572470936999
25 Definicion del Numero Aureo
El número áureo o también conocido como número Phi, es una constante de base 10 muy utilizada en matemáticas.
La constante áurea es un número irracional de base 10 , como lo son el número E, o PI ya que contiene infinidad de decimales.
La constante áurea se calcula de la siguiente manera:
- Constante Aurea ( 1,618033988 ) = ((5yRoot2)+1)/2
El número áureo o constante Phi con 49 decimales es el siguiente:
- { 1,6180339887498948482045868343656381177203091798057 }
Puntuación del Autor: 
